Пути через таблицу

Начиная в левом верхнем углу сетки 2×2 и имея возможность двигаться только вниз или вправо, существует ровно 6 маршрутов до правого нижнего угла сетки.

Сколько существует таких маршрутов в сетке 20×20?

Решение (F#)

• для того, чтобы пройти таблицу N x N, необходимо пройти N клеток вправо и N клеток вниз, совершив при этом 2N передвижений
• итак имеем 2N шагов из них N вправо, остальные (N) - вниз
• рассмотрим пример для таблицы 3х3: всего нужно сделать 6 шагов - 3 вправо и 3 вниз в любой последовательности, обозначим движение вниз синим цветом, всего получим 20 возможных путей

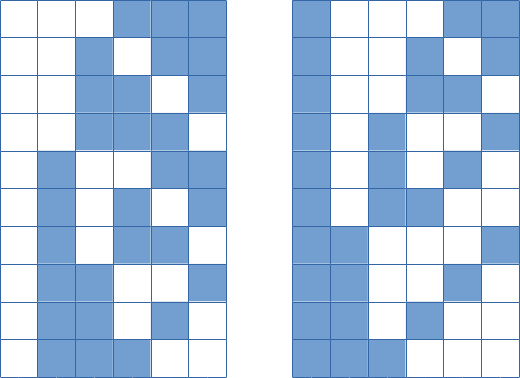
• это ничто иное как сочетания из 6 по 3, значит для решения не будем перебирать все возможные маршруты а воспользуемся формулой числа сочетаний: Число сочетаний из N по K равно биномиальному коэффициенту N! / ( K! * (N-K)! )
• для N=6 и K=3 получим 1*2*3*4*5*6/(1*2*3 * 1*2*3) = 20
• тогда код решения будет весьма тривиален:
  • объявляем рекурсивную функцию нахождения факториала fact, здесь нет хвостовой рекурсии - нет смысла усложнять, потому что максимальная глубина рекурсии не превышает 40 в нашем случае
  • считаем 40!/(20! * 20!)
  • выводим ответ

let rec fact n = 
  if n=1 then bigint 1 else bigint n * fact (n-1)

let answer =
  let f20 = fact 20
  (fact 40)/(f20*f20)

printfn $"the answer is {answer:N0}" //the answer is 137 846 528 820

• bigint используется из-за того, что промежуточные числа не входят в int64